
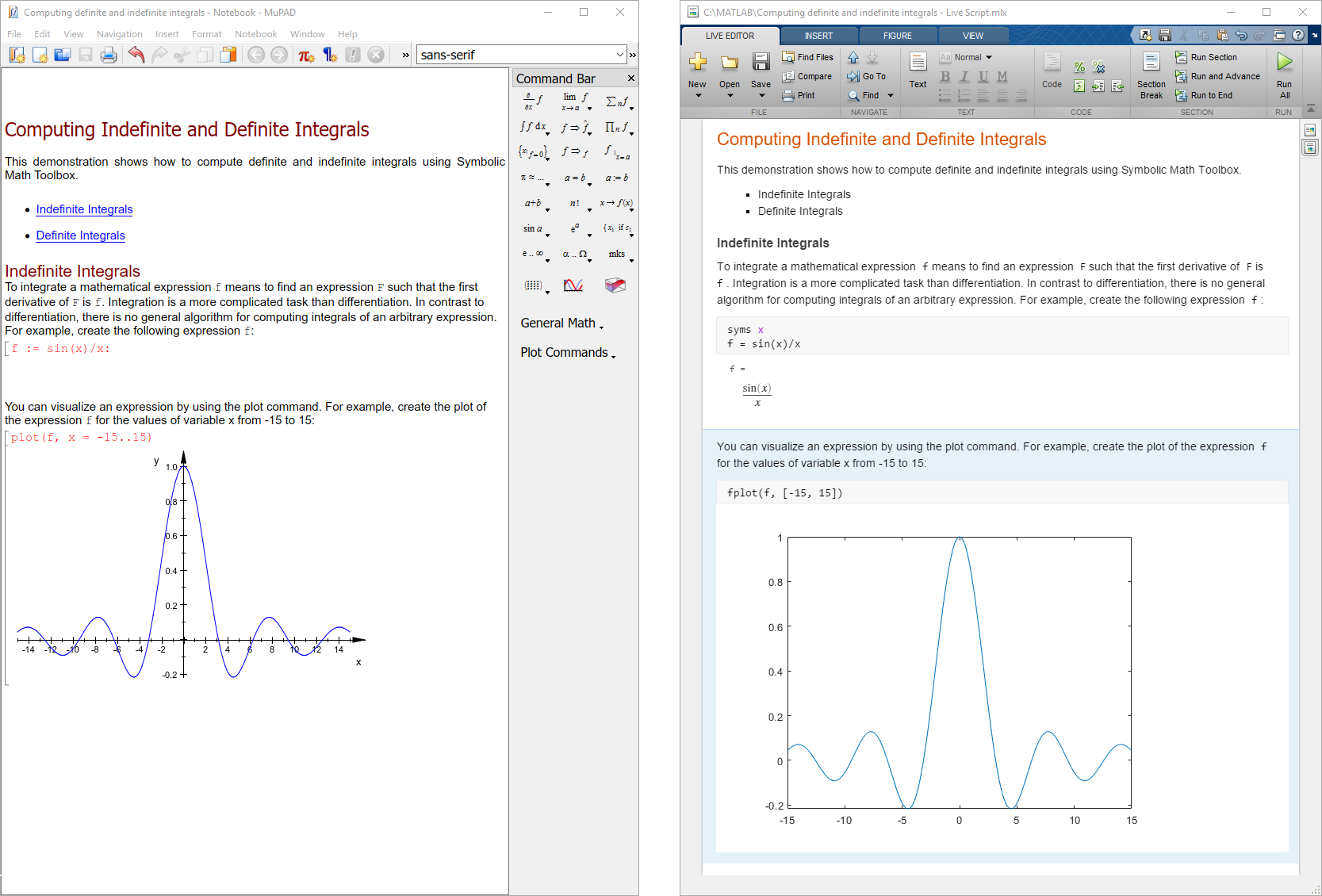

This installation supports distributed and parallel computing across 8 “workers” using the Distributed Computing Engine. Hence, it is safe to call your result real.Only a single user license for each, for now … the Engine can invoke up to 8 “workers” which can run simultaneously without checking out licenses. Ideally it may be zero and it's coming due to imprecise calculations.

This implies that the imaginary part is extremely small and it is not a considerable amount to be worried about. Let's check the maximum value of imaginary part in yk. Now let's check the imaginary part of the result we have: > imag(yk) Yk(k-4) = subs(y,x,k) %Putting the value of x
Now put some real values of x≥5 to check what result it gives: n = 1004 %We'll be putting 1000 values of x in y from 5 to 1004 Take a look at this: clear all %To clear the conditions of x as real and >=5 (simple clear doesn't clear that) Using the symbolic real form above should avoid this. Which returns 5*atan2(5, (x^2-25)^(1/2)) + (x^2-25)^(1/2).Īlso, as points out, when the full solution is converted to floating point (or variable precision) there will sometimes numeric imprecision when converting from exact symbolic form. If you want to get rid of the zero-valued imaginary part of the solution you can use sym/real: real(y) You might also submit this case to The MathWorks as a service request in case they'd consider improving the simplification for this and similar equations. Unfortunately, Matlab's simplification routines appear to not be able to reduce this expression when assumptions are included. Or you can use more symbolic math via the isAlways function to show this: syms x real With a bit of math you can show that the solution is always real for x>=5 (see complex logarithm). This solution is valid over the entire domain of of real values, including your restricted domain of x>=5. This occurs because Matlab's int function returns the full general solution when you ask for the indefinite integral. This behavior is present in R2017b, though when converted to floating point the imaginary components are different.


 0 kommentar(er)
0 kommentar(er)
